发表于 | 分类于 ， | 阅读次数:

一、功能说明：

  • 想点击一个按钮，折叠/展开一个widget

二、预览

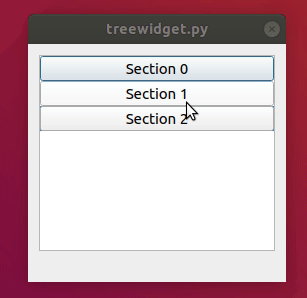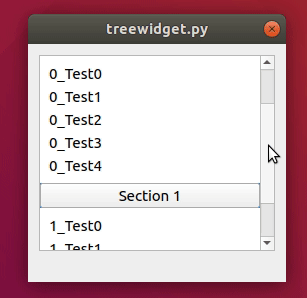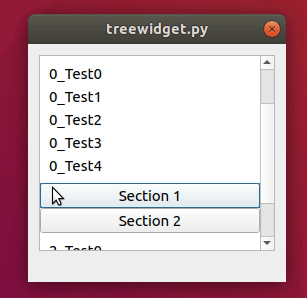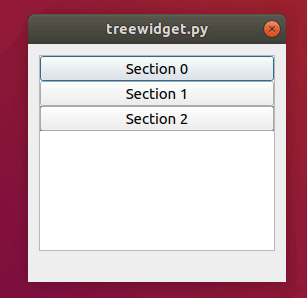
fold折叠QWidget

三、PyQt5代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
# -*- coding:utf-8 -*-
"""
@Author: lamborghini
@Date: 2019-01-08 21:07:07
@Desc: 可折叠widget
"""

import sys
from PyQt5.QtWidgets import (QPushButton, QDialog, QTreeWidget,
                             QTreeWidgetItem, QVBoxLayout,
                             QHBoxLayout, QFrame, QLabel,
                             QApplication, QSpacerItem,
                             QSizePolicy, QHeaderView)


class SectionExpandButton(QPushButton):
    """
    a QPushbutton that can expand or collapse its section
    """

    def __init__(self, item, text="", parent=None):
        super().__init__(text, parent)
        self.section = item
        self.clicked.connect(self.on_clicked)

    def on_clicked(self):
        """
        toggle expand/collapse of section by clicking
        """
        if self.section.isExpanded():
            self.section.setExpanded(False)
        else:
            self.section.setExpanded(True)


class CollapsibleDialog(QDialog):
    """
    a dialog to which collapsible sections can be added;
    subclass and reimplement define_sections() to define sections and
        add them as (title, widget) tuples to self.sections
    """

    def __init__(self):
        super().__init__()
        self.tree = QTreeWidget()
        self.tree.setHeaderHidden(True)
        layout = QVBoxLayout()
        item = QSpacerItem(67, 20, QSizePolicy.Expanding, QSizePolicy.Minimum)
        layout.addWidget(self.tree)
        layout.addItem(item)
        self.setLayout(layout)
        self.tree.setIndentation(0)

        self.sections = []
        self.define_sections()
        self.add_sections()

    def add_sections(self):
        """
        adds a collapsible sections for every 
        (title, widget) tuple in self.sections
        """
        for (title, widget) in self.sections:
            button1 = self.add_button(title)
            section1 = self.add_widget(button1, widget)
            button1.addChild(section1)

    def define_sections(self):
        """
        reimplement this to define all your sections
        and add them as (title, widget) tuples to self.sections
        """
        for x in range(3):
            widget = QFrame(self.tree)
            vbox = QVBoxLayout(widget)  # fold widget
            for y in range(5):
                sName = "%s_Test%s" % (x, y)
                label = QLabel(sName, widget)
                vbox.addWidget(label)
            widget.setLayout(vbox)
            title = "Section %s" % x
            self.sections.append((title, widget))

    def define_sections2(self):
        """
        reimplement this to define all your sections
        and add them as (title, widget) tuples to self.sections
        """
        for x in range(3):
            widget = QTreeWidget(self.tree) # fold QTreeWidget
            widget.setHeaderHidden(True)
            widget.header().setSectionResizeMode(QHeaderView.Stretch)
            for y in range(5):
                sName = "%s_Test%s" % (x, y)
                item = QTreeWidgetItem(widget)
                item.setText(0, sName)
            title = "Section %s" % x
            self.sections.append((title, widget))

    def add_button(self, title):
        """
        creates a QTreeWidgetItem containing a button 
        to expand or collapse its section
        """
        item = QTreeWidgetItem()
        self.tree.addTopLevelItem(item)
        self.tree.setItemWidget(item, 0, SectionExpandButton(item, text=title))
        return item

    def add_widget(self, button, widget):
        """
        creates a QWidgetItem containing the widget,
        as child of the button-QWidgetItem
        """
        section = QTreeWidgetItem(button)
        section.setDisabled(True)
        self.tree.setItemWidget(section, 0, widget)
        return section


if __name__ == "__main__":
    app = QApplication(sys.argv)
    window = CollapsibleDialog()
    window.show()
    sys.exit(app.exec_())

发表于 | 分类于 | 阅读次数:

题目地址

题意：

运用你所掌握的数据结构，设计和实现一个 LRU (最近最少使用) 缓存机制。它应该支持以下操作： 获取数据 get 和 写入数据 put 。

获取数据 get(key) - 如果密钥 (key) 存在于缓存中，则获取密钥的值（总是正数），否则返回 -1。
写入数据 put(key, value) - 如果密钥不存在，则写入其数据值。当缓存容量达到上限时，它应该在写入新数据之前删除最近最少使用的数据值，从而为新的数据值留出空间。

进阶:

你是否可以在 O(1) 时间复杂度内完成这两种操作？

示例:

LRUCache cache = new LRUCache( 2 / 缓存容量 / );

cache.put(1, 1);
cache.put(2, 2);
cache.get(1); // 返回 1
cache.put(3, 3); // 该操作会使得密钥 2 作废
cache.get(2); // 返回 -1 (未找到)
cache.put(4, 4); // 该操作会使得密钥 1 作废
cache.get(1); // 返回 -1 (未找到)
cache.get(3); // 返回 3
cache.get(4); // 返回 4

解题思路：

  • 这里其实就是想实现一个有序字典
  • 可以使用list（列表） + unordered_map（hash表）来实现
  • get：判断是否在列表中
    • 如果不在返回-1
    • 如果在，删除node，然后添加到列表第一位，返回结果
  • put：判断是否在列表中
    • 如果在，删除node，然后添加到列表第一位
    • 不在，添加到列表中，如果越界删除最后一位

C++代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <string>
#include <queue>
#include <climits>
#include <algorithm>
#include <map>
#include <unordered_map>
#include <list>
using namespace std;

class LRUCache
{
  public:
    struct _node
    {
        int _key;
        int _val;
        _node(int k, int v) : _val(v), _key(k){};
    };

  public:
    list<_node> _list;
    unordered_map<int, list<_node>::iterator> keynode;
    int _maxsize;
    int _cursize;
    LRUCache(int capacity)
    {
        _maxsize = capacity;
        _cursize = 0;
    }

    int get(int key)
    {
        if (_cursize == 0)
        {
            return -1;
        }
        if (keynode.find(key) != keynode.end())
        {
            int res = keynode[key]->_val;
            _list.erase(keynode[key]);
            _list.push_front(_node(key, res));
            keynode[key] = _list.begin();
            return res;
        }
        return -1;
    }

    void put(int key, int value)
    {
        if (keynode.find(key) != keynode.end())
        {
            _list.erase(keynode[key]);
            _list.push_front(_node(key, value));
            keynode[key] = _list.begin();
            return;
        }
        _cursize++;
        if (_cursize <= _maxsize)
        {
            _list.push_front(_node(key, value));
            keynode[key] = _list.begin();
        }
        else
        {
            _list.push_front(_node(key, value));
            int rkey = (--_list.end())->_key;
            keynode.erase(rkey);
            keynode[key] = _list.begin();
            _list.pop_back();
        }
    }
};

python代码：

  • python的话直接用OrderedDict 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    # -*- coding:utf-8 -*-
    """
    @Author: lamborghini
    @Date: 2018-12-26 19:54:05
    @Desc: LRU缓存机制
    """

    from collections import OrderedDict


    class LRUCache:

        def __init__(self, capacity):
            """
            :type capacity: int
            """
            self.m_Cap = capacity
            self.m_Cnt = 0
            self.m_Info = OrderedDict()

        def get(self, key):
            """
            :type key: int
            :rtype: int
            """
            if key in self.m_Info:
                val = self.m_Info[key]
                del self.m_Info[key]
                self.m_Info[key] = val
                return val
            return -1

        def put(self, key, value):
            """
            :type key: int
            :type value: int
            :rtype: void
            """
            if key in self.m_Info:
                del self.m_Info[key]
                self.m_Info[key] = value
                return
            self.m_Cnt += 1
            self.m_Info[key] = value
            if self.m_Cnt > self.m_Cap:
                for key in self.m_Info:
                    del self.m_Info[key]
                    return

    # Your LRUCache object will be instantiated and called as such:
    # obj = LRUCache(capacity)
    # param_1 = obj.get(key)
    # obj.put(key,value)

github

发表于 | 分类于 | 阅读次数:

题目地址

题意：

给定一个非空二叉树，返回其最大路径和。

本题中，路径被定义为一条从树中任意节点出发，达到任意节点的序列。该路径至少包含一个节点，且不一定经过根节点。

示例 1:

输入: [1,2,3]

  1
 / \
2   3

输出: 6

示例 2:

输入: [-10,9,20,null,null,15,7]

   -10
   / \
  9  20
 /  \
15   7

输出: 42

解题思路：

  • 要求一条路径的最大值，可以从任意节点出发，转化为：
  1. 从底层开始遍历，每次修改当前节点的值为max(当前节点、当前节点+左节点、当前节点+右节点、当前节点+左右节点)
  2. 每次遍历时并记录最大值

代码一：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <string>
#include <queue>
#include <climits>
#include <algorithm>
using namespace std;

struct TreeNode
{
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

class Solution
{
  public:
    int result = INT_MIN;
    int maxPathSum(TreeNode *root)
    {
        DFS(root);
        return result;
    }

    void DFS(TreeNode *temp)
    {
        int o, a = 0, b = 0;
        o = temp->val;
        if (temp->left)
        {
            DFS(temp->left);
            a = temp->left->val;
        }
        if (temp->right)
        {
            DFS(temp->right);
            b = temp->right->val;
        }
        printf("%d %d %d %d", o, a, b, result);
        // 求最大值
        result = max(result, o);
        result = max(result, o + a);
        result = max(result, o + b);
        result = max(result, o + a + b);
        printf("----%d\n", result);
        // 算出当前节点最大的值
        temp->val = max(o, o + b);
        temp->val = max(temp->val, o + a);
    }
};

优化代码二：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <string>
#include <queue>
#include <climits>
#include <algorithm>
using namespace std;

struct TreeNode
{
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

class Solution
{
  public:
    int result = INT_MIN;
    int maxPathSum(TreeNode *root)
    {
        DFS(root);
        return result;
    }

    int DFS(TreeNode *temp)
    {
        if (temp == NULL)
            return 0;
        int left, right;
        left = max(0, DFS(temp->left));
        right = max(0, DFS(temp->right));
        result = max(result, temp->val + left + right);
        return max(temp->val, temp->val + max(left, right));
    }
};

github

发表于 | 分类于 | 阅读次数:

题目地址

题意：

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

例如，上图是一个7 x 3 的网格。有多少可能的路径？

说明：m 和 n 的值均不超过 100。

示例 1:

输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。

  1. 向右 -> 向右 -> 向下
  2. 向右 -> 向下 -> 向右
  3. 向下 -> 向右 -> 向右

示例 2:

输入: m = 7, n = 3
输出: 28

解题思路一：

  • 可以递推出dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
  • 所以显然可以直接用动态规划解决
  • 这里其实可以优化为两个一维数组，因为每次进行for循环只和上一次有关系

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <string>
#include <queue>
#include <climits>
#include <algorithm>
using namespace std;

class Solution
{
  public:
    int uniquePaths(int m, int n)
    {
        int dp[110][110];
        int i, j;
        memset(dp, sizeof(dp), 0);
        for (i = 0; i < m; i++)
            dp[i][0] = 1;
        for (i = 0; i < n; i++)
            dp[0][i] = 1;
        for (i = 1; i < m; i++)
            for (j = 1; j < n; j++)
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        return dp[m-1][n-1];
    }
};

int main(int argc, char const *argv[])
{
    printf("%d\n", Solution().uniquePaths(7, 3));
    return 0;
}

解题思路二：

  • 因为只能往下和往右，总的步数为n+m-2
  • 所以可以转化为求在n+m-2中求n-1次往右走，或者m-1次往下走的情况
  • 所以结果为C(n+m-2, n-1)或者C(n+m-2, m-1)

github

发表于 | 分类于 | 阅读次数:

题目地址

题意：

给定一个链表，旋转链表，将链表每个节点向右移动 k 个位置，其中 k 是非负数。

示例 1:

输入: 1->2->3->4->5->NULL, k = 2
输出: 4->5->1->2->3->NULL
解释:
向右旋转 1 步: 5->1->2->3->4->NULL
向右旋转 2 步: 4->5->1->2->3->NULL

示例 2:

输入: 0->1->2->NULL, k = 4
输出: 2->0->1->NULL
解释:
向右旋转 1 步: 2->0->1->NULL
向右旋转 2 步: 1->2->0->NULL
向右旋转 3 步: 0->1->2->NULL
向右旋转 4 步: 2->0->1->NULL

解题思路：

  1. 遍历链表，记录末位链表指针，以及链表长度:cnt
  2. 因为旋转的长度可能大于链表的长度，所以需要做如下处理t=(cnt - k % cnt) % cnt
  3. 然后将前t个放到末位即可

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <cstring>
#include <string>
#include <queue>
#include <climits>
#include <algorithm>
using namespace std;

struct ListNode
{
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(NULL) {}
};

class Solution
{
  public:
    ListNode *rotateRight(ListNode *head, int k)
    {
        ListNode *tmp = head, *tail;
        int cnt = 0; //  链表长度
        while (tmp)
        {
            cnt++;
            tail = tmp;
            tmp = tmp->next;
        }
        if (cnt == 0)
            return head;
        int t = (cnt - k % cnt) % cnt; // 移动的次数
        if (t == 0)
            return head;
        tail->next = head; // 将链表指向头
        while (t--)
        {
            tmp = head;
            head = head->next;
        }
        tmp->next = NULL;
        return head;
    }
};

github

发表于 | 分类于 | 阅读次数:

题目地址

题意：

给定两个以字符串形式表示的非负整数 num1 和 num2，返回 num1 和 num2 的乘积，它们的乘积也表示为字符串形式。

示例 1:

输入: num1 = “2”, num2 = “3”
输出: “6”

示例 2:

输入: num1 = “123”, num2 = “456”
输出: “56088”

说明：

num1 和 num2 的长度小于110。
num1 和 num2 只包含数字 0-9。
num1 和 num2 均不以零开头，除非是数字 0 本身。
不能使用任何标准库的大数类型（比如 BigInteger）或直接将输入转换为整数来处理。

解题思路：

  • 简单的说就是大数相乘
  1. 将字符串转为数字用数组逆序（方便计算乘法）存起来
  2. 一一相乘两个数组，然后放到新数组中，记得做进位处理
    1
    2
    3
    tmp = result[i + j] + n1[i] * n2[j];
    result[i + j] = tmp % 10;
    result[i + j + 1] += tmp / 10;
  • 代码如下： 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    #include <iostream>
    #include <cstdio>
    #include <cmath>
    #include <cstdlib>
    #include <cstring>
    #include <string>
    #include <queue>
    #include <climits>
    #include <algorithm>
    using namespace std;

    class Solution
    {
      public:
        int i, j, l1, l2, tmp;
        int result[222], n1[111], n2[111];

        string multiply(string num1, string num2)
        {
            l1 = num1.length();
            for (i = 0; i < l1; i++)
                n1[i] = num1[l1 - 1 - i] - '0';
            l2 = num2.length();
            for (i = 0; i < l2; i++)
                n2[i] = num2[l2 - 1 - i] - '0';
            Print(n1, l1);
            Print(n2, l2);
            memset(result, sizeof(result), 0);
            for (i = 0; i < l1; i++)
            {
                for (j = 0; j < l2; j++)
                {
                    tmp = result[i + j] + n1[i] * n2[j];
                    result[i + j] = tmp % 10;
                    result[i + j + 1] += tmp / 10;
                }
            }
            Print(result, l1 + l2);
            string re = "";
            tmp = l1 + l2;
            while (tmp >= 1 && result[tmp] == 0)
            {
                tmp--; //排除末位0
            }
            for (i = tmp; i >= 0; i--)
            {
                re += result[i] + '0';
            }
            cout << re << endl;
            return re;
        }

        void Print(int t[], int size)
        {
            for (int i = 0; i < size; i++)
            {
                printf("%d", t[i]);
            }
            printf("\n");
        }
    };

    int main(int argc, char const *argv[])
    {
        string s1 = "123", s2 = "456";
        Solution().multiply(s1, s2);
        return 0;
    }

github

发表于 | 分类于 | 阅读次数:

题目地址

题意：

合并 k 个排序链表，返回合并后的排序链表。请分析和描述算法的复杂度。
示例:

输入:
[
1->4->5,
1->3->4,
2->6
]

输出: 1->1->2->3->4->4->5->6

C++中.和->区别

好久没写C++，现在准备捡回来

c++中当定义类对象是指针对象时候，就需要用到 “->” 指向类中的成员；

当定义一般对象时候时就需要用到 “.” 指向类中的成员……

例如：

1
2
3
4
5
6
7
8
struct MyStruct
{ 
    int member; 
};
MyStruct a, *p;
a.member = 1;
p->member = 1;
(*p).member =1

总结：

  • 箭头（->）：左边必须为指针；
  • 点号（.）：左边必须为实体。

解题思路一：

  • 将所有数字放到一个列表里，然后用快排 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    78
    79
    80
    #include <iostream>
    #include <cstdio>
    #include <cmath>
    #include <cstdlib>
    #include <cstring>
    #include <string>
    #include <queue>
    #include <climits>
    #include <algorithm>
    using namespace std;

    struct ListNode
    {
        int val;
        ListNode *next;
        ListNode(int x) : val(x), next(NULL) {}
    };
    vector<ListNode *> mylists;
    int i;

    ListNode *AddListNode(int t[], int size)
    {
        ListNode *head = NULL, *first = NULL, *current = NULL;
        if(size==0)
            return head;
        head = first = new ListNode(t[0]);
        for (int i = 1; i < size; i++)
        {
            current = new ListNode(t[i]);
            first->next = current;
            first = first->next;
        }
        mylists.push_back(head);
        return head;
    }

    class Solution
    {
      public:
        ListNode *mergeKLists(vector<ListNode *> &lists)
        {
            ListNode *result = NULL;
            if(lists.size() == 0)
                return result;
            int t[999999], cnt = 0;
            for (i = 0; i < lists.size(); i++)
            {
                while (lists[i])
                {
                    t[cnt++] = lists[i]->val;
                    lists[i] = lists[i]->next;
                }
            }
            sort(t, t + cnt);
            for (i = 0; i < cnt; i++)
                cout << t[i] << " ";
            cout << endl;
            ListNode *head = AddListNode(t, cnt);
            result = head;
            while (head)
            {
                cout << head->val << "->";
                head = head->next;
            }
            cout << endl;
            return result;
        }
    };

    int main(int argc, char const *argv[])
    {
        int t1[] = {1, 4, 5};
        int t2[] = {1, 3, 4};
        int t3[] = {2, 6};
        AddListNode(t1, 3);
        AddListNode(t2, 3);
        AddListNode(t3, 2);
        ListNode *result = Solution().mergeKLists(mylists);
        return 0;
    }

解题思路二：

  • 我们知道如果是将两个有序列表合并成一个有序列表就很简单了。
  • 所以可以使用归并排序的思想，每次进行两两合并。 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    78
    79
    80
    81
    82
    83
    84
    85
    86
    87
    88
    89
    90
    91
    92
    93
    94
    95
    96
    97
    98
    99
    100
    101
    102
    103
    104
    105
    106
    107
    108
    109
    110
    #include <iostream>
    #include <cstdio>
    #include <cmath>
    #include <cstdlib>
    #include <cstring>
    #include <string>
    #include <queue>
    #include <climits>
    #include <algorithm>
    using namespace std;

    struct ListNode
    {
        int val;
        ListNode *next;
        ListNode(int x) : val(x), next(NULL) {}
    };
    vector<ListNode *> mylists;

    ListNode *AddListNode(int t[], int size)
    {
        ListNode *head = NULL, *first = NULL, *current = NULL;
        if (size == 0)
            return head;
        head = first = new ListNode(t[0]);
        for (int i = 1; i < size; i++)
        {
            current = new ListNode(t[i]);
            first->next = current;
            first = first->next;
        }
        mylists.push_back(head);
        return head;
    }

    class Solution
    {
      public:
        int i, t, lsize;

        ListNode *mergeKLists(vector<ListNode *> &lists)
        {
            if (lists.size() == 0)
                return NULL;
            lsize = lists.size();
            // 归并合并
            while (lsize > 1)
            {
                t = (1 + lsize) / 2;
                for (i = 0; i < lsize / 2; i++)
                {
                    lists[i] = mergeTwoLists(lists[i], lists[i + t]);
                    // printf("mergeTwoLists %d:", i);
                    // nodeprint(lists[i]);
                }
                lsize = t;
            }
            return lists[0];
        }

        ListNode *mergeTwoLists(ListNode *l1, ListNode *l2)
        {
            ListNode *head, *cur;
            head = cur = new ListNode(0);
            // nodeprint(l1);
            // nodeprint(l2);
            while (l1 && l2)
            {
                if (l1->val > l2->val)
                {
                    cur->next = l2;
                    l2 = l2->next;
                }
                else
                {
                    cur->next = l1;
                    l1 = l1->next;
                }
                cur = cur->next;
            }
            if (l1)
                cur->next = l1;
            if (l2)
                cur->next = l2;
            // nodeprint(head->next);
            return head->next;
        }

        void nodeprint(ListNode *print)
        {
            while (print)
            {
                cout << print->val << " ";
                print = print->next;
            }
            cout << endl;
        }
    };

    int main(int argc, char const *argv[])
    {
        int t1[] = {1, 4, 5};
        int t2[] = {1, 3, 4};
        int t3[] = {2, 6};
        AddListNode(t1, 3);
        AddListNode(t2, 3);
        AddListNode(t3, 2);
        ListNode *result = Solution().mergeKLists(mylists);
        return 0;
    }

github

发表于 | 分类于 | 阅读次数:

题目地址

题意：

给定一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？找出所有满足条件且不重复的三元组。

注意：答案中不可以包含重复的三元组。

例如, 给定数组 nums = [-1, 0, 1, 2, -1, -4]，

满足要求的三元组集合为：

[
[-1, 0, 1
[-1, -1, 2]
]

解题思路：

  • 很显然进行三重遍历会超时。
  • 这里我们可以取一个数a，然后其他两个数b，c使得a+b+c=0即可
  • 找bc我们可以先进行排序，然后从两边往中间扫，使a+b+c=0
  • 这里注意记得去重（相同就跳过就行） 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    package main

    import (
    	"fmt"
    	"sort"
    )

    func threeSum(nums []int) [][]int {
    	sort.Ints(nums)
    	var items [][]int
    	var i,j,k,s int
    	for i = 0; i < len(nums); i++ {
    		if i != 0 && nums[i] <= nums[i-1] {
    			continue	// 去重相同的
    		}
    		j = i + 1
    		k = len(nums) - 1
    		for j < k {
    			s = nums[i] + nums[j] + nums[k]
    			if s == 0 {
    				tmp := []int{nums[i], nums[j], nums[k]}
    				items = append(items, tmp)
    				j += 1
    				k -= 1
    				for j < k && nums[j] == nums[j-1] {	
    					j += 1	 // 去重相同的
    				}
    				for j < k && nums[k] == nums[k+1] {	
    					k -= 1	// 去重相同的
    				}
    			} else if s < 0 {
    				j += 1
    			} else {
    				k -= 1
    			}
    		}
    	}
    	return items
    }

    func main() {
    	nums := []int{-1, 0, 1, 2, -1, -4}
    	fmt.Println(threeSum(nums))
    	nums = []int{0,0,0}
    	fmt.Println(threeSum(nums))
    }

github

发表于 | 分类于 | 阅读次数:

题目地址

题意：

假设按照升序排序的数组在预先未知的某个点上进行了旋转。

( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。

搜索一个给定的目标值，如果数组中存在这个目标值，则返回它的索引，否则返回 -1 。

你可以假设数组中不存在重复的元素。

你的算法时间复杂度必须是 O(log n) 级别。

示例 1:

输入: nums = [4,5,6,7,0,1,2], target = 0
输出: 4

示例 2:

输入: nums = [4,5,6,7,0,1,2], target = 3
输出: -1

解题思路：

因为是递增的一次旋转数组，所以我们也可以用二分+我们特殊的判断来做

  • 如果二分到是正常的递增，那么按照正常的逻辑进行
  • 否则继续按照一次旋转数组进行判断二分：
    • 左边是正常递增，如果目标在左边，则r=m-1，否则l=m+1
    • 右边是正常递增，如果目标在右边，则l=m+1，否则r=m-1
  • 每次记得判断中数是否是寻找的值，是就直接返回 
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    #include <iostream>
    #include <cstdio>
    #include <cmath>
    #include <cstdlib>
    #include <cstring>
    #include <string>
    #include <queue>
    #include <climits>
    #include <algorithm>
    using namespace std;

    class Solution
    {
      public:
        int l, r, m;
        bool left;
        int search(vector<int> &nums, int target)
        {
            l = 0;
            r = nums.size() - 1;
            while (l <= r)
            {
                m = (l + r) / 2;
                printf("mid %d %d %d\n", l, m, r);
                if (nums[m] == target)
                    return m;

                if (nums[l] < nums[r]) // 正常递增
                {
                    if (nums[m] > target)
                        r = m - 1;
                    else
                        l = m + 1;
                }
                else // 非正常递增
                {
                    if (nums[l] <= nums[m]) // 左边是正常递增
                    {
                        if (nums[l] <= target && target < nums[m])
                            r = m - 1;
                        else
                            l = m + 1;
                    }
                    else // 右边是正常递增
                    {
                        if (nums[m] < target && target <= nums[r])
                            l = m + 1;
                        else
                            r = m - 1;
                    }
                }
            }
            return -1;
        }
    };

    int main(int argc, char const *argv[])
    {
        int t[] = {4, 5, 6, 7, 0, 1, 2};
        vector<int> p;
        int iLen = sizeof(t) / sizeof(t[0]);
        for (int i = 0; i < iLen; i++)
            p.push_back(t[i]);
        cout << Solution().search(p, 2) << endl;
        return 0;
    }

github

发表于 | 分类于 | 阅读次数:

题目地址

题意：

给定一个包括 n 个整数的数组 nums 和 一个目标值 target。找出 nums 中的三个整数，使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。

例如，给定数组 nums = [-1，2，1，-4], 和 target = 1.

与 target 最接近的三个数的和为 2. (-1 + 2 + 1 = 2).

解题思路：

  • 碰到这种问题解决方法：
    1. 排序
    2. 遍历一个数据i，将三数求和变为两数求和
    3. j = i + 1, k = len - 1 从两头开始遍历
  • 每次遍历和target比较大小，
    1. < target时，j++，并且比较当前相差最小值+记录
    2. > target时，k–，并且记录当前相差最小值+记录
    3. = target时，直接返回target 
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      26
      27
      28
      29
      30
      31
      32
      33
      34
      35
      36
      37
      38
      39
      40
      41
      42
      43
      44
      45
      46
      47
      48
      49
      50
      51
      52
      53
      54
      55
      56
      57
      58
      59
      60
      61
      62
      63
      64
      65
      66
      67
      68
      69
      70
      71
      72
      73
      74
      75
      76
      77
      78
      #include <iostream>
      #include <cstdio>
      #include <cmath>
      #include <cstdlib>
      #include <cstring>
      #include <string>
      #include <queue>
      #include <climits>
      #include <algorithm>
      using namespace std;

      class Solution
      {
        public:
          int value, minCha = INT_MAX, t;

          void Compare(int tmp, int target)
          {
              t = abs(tmp - target);
              if (t < minCha)
              {
                  minCha = t;
                  value = tmp;
              }
          }

          int threeSumClosest(vector<int> &nums, int target)
          {
              int i, j, k, tmp;
              sort(nums.begin(), nums.end());
              for (int i = 0; i < nums.size(); i++)
                  cout << nums[i] << " ";
              cout << endl;

              for (i = 0; i < nums.size(); i++)
              {
                  j = i + 1;
                  k = nums.size() - 1;

                  while (j < k)
                  {
                      tmp = nums[j] + nums[k] + nums[i];
                      if (tmp > target)
                      {
                          k--;
                          Compare(tmp, target);
                      }
                      else if (tmp < target)
                      {
                          Compare(tmp, target);
                          j++;
                      }
                      else
                      {
                          printf("%d %d %d %d %d\n", i, j, k, tmp, target);
                          return tmp;
                      }
                  }
              }
              return value;
          }
      };

      int main(int argc, char const *argv[])
      {
          // int t[] = {-1, 2, 1, -4};
          // int iLen = sizeof(t) / sizeof(t[0]);
          // vector<int> p(t, t + iLen);
          // Solution obj = Solution();
          // printf("%d\n", obj.threeSumClosest(p, 1));

          int t[] = {0, 1, 2};
          int iLen = sizeof(t) / sizeof(t[0]);
          vector<int> p(t, t + iLen);
          Solution obj = Solution();
          printf("%d\n", obj.threeSumClosest(p, 3));
          return 0;
      }

github